Hamming codes
Below is an example of the (7,4) Hamming code. The bits s₁s₂s₃s₄ are the source bits, and the bits t₅t₆t₇ are the parity bits. The parity bits are set such that the parity of the bits within each circle is even (zero since each bit can be either 1 or 0). The transmitted codeword can be represented by the matrix 𝐭=\begin{bmatrix} s₁&s₂&s₃&s₄ &t₅&t₆&t₇\end{bmatrix}^⊺.
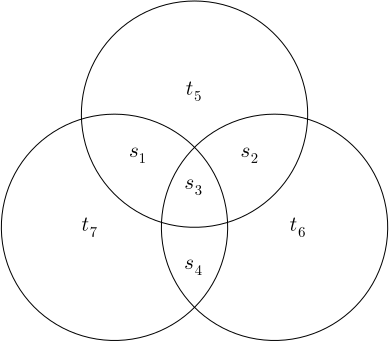
We have
\begin{align*} s_1 \oplus s_3 \oplus s_4 \oplus t_7 = 0,& \\ s_1 \oplus s_2 \oplus s_3 \oplus t_5 = 0,&\text{ and }\\ s_2 \oplus s_3 \oplus s_4 \oplus t_6 = 0,& \\ \end{align*}
where \oplus is addition modulo 2. Then s_1 \oplus s_3 \oplus s_4 = t_7 and so on. In matrix form this is expressed as
𝐭=𝐆^T𝐬 =\begin{bmatrix} 𝐈_4 \\ 𝐏 \end{bmatrix}𝐬, \quad\text{ with } 𝐏=\begin{bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \end{bmatrix}.
Decoding is then the reverse process. The syndrome is given by 𝐇𝐭=\begin{bmatrix}𝐏 & 𝐈_3 \end{bmatrix}𝐭.
Assuming each of t_5t_6t_7 has not been flipped, the syndrome identifies which bit of s_1s_2s_3s_4 should be flipped to make the parity even again. For example, if the syndrome is \begin{bmatrix}1 & 1 & 0\end{bmatrix}^T, then the syndromes involving s_1s_2s_3t_5 and s_2s_3s_4t_5 have odd parity. Flipping either s_2 or s_3 would make these syndroms even parity, but flipping s_3 would affect the other syndrome, so s_2 is flipped.
Some code that implements a (7,4) Hamming encoder/decoder is given below.
P = [1 1 1 0; 0 1 1 1; 1 0 1 1]
I₄ = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]
I₃ = [1 0 0; 0 1 0; 0 0 1]
encode(s::Vector{T}) where {T} = vcat(I₄, P)*s .% 2
decode(t::Vector{T}) where {T} = begin
syndrome = hcat(P, I₃)*t .% 2
if syndrome == [1;0;1]
t = (t + [1; 0; 0; 0; 0;0;0]) .% 2
elseif syndrome == [1;1;0]
t = (t + [0; 1; 0; 0; 0;0;0]) .% 2
elseif syndrome == [1;1;1]
t = (t + [0; 0; 1; 0; 0;0;0]) .% 2
elseif syndrome == [0;1;1]
t = (t + [0; 0; 0; 1; 0;0;0]) .% 2
end
return t[1:4]
end
@test encode([0;1;0;0]) == [0;1;0;0;1;1;0]
@test decode([0;1;0;0;1;1;0]) == [0;1;0;0]
@test decode([0;1;1;0;1;1;0]) == [0;1;0;0]Encoding a picture of an owl, adding some noise with probability
0.1, and decoding the picture again
gives the following result. 